画像処理とか機械学習とか

画像処理や機械学習関連の事について気まぐれで書いていきます。歩行者検出関係が多いと思います。ハリネズミもたまに出現します。

EMアルゴリズム

機械学習

今回は、前回の混合ガウスモデルに引き続き、混合ガウスモデルのパラメータ推定の手法に使えるEMアルゴリズムについて紹介したいと思います。

混合ガウスモデルを例に挙げますので、混合ガウスモデルが分からない方は前回の記事を参照してください。
hiro2o2.hatenablog.jp

混合ガウスモデルは以下の式で表せました。
{ \displaystyle p(x|\theta)=\sum_{j=1}^K \pi_jN(x|\mu_j,\Sigma_j) }
何か近似したい確率密度分布（真の分布）がある際に、混合ガウスモデルを使って近似する場合、最も真の分布に近づくような、パラメータ{ \displaystyle \theta }が分かれば良いです。

このパラメータ{ \displaystyle \theta }の学習に、通常のガウスモデルと同じように最尤推定を用い、対数尤度の最大化のアプローチで解けるでしょうか？

{ \displaystyle \hat{\theta}={\rm argmax}\sum_{i=1}^I\log(p(x_i|\theta))\\ ={\rm argmax}\sum_{i=1}^I\log(\sum_{j=1}^K\pi_jN(x_i|\mu_j,\Sigma_j)) }

このように、正規分布の和のlogの部分で、微分して0とおく計算が難しくなります。
また、重み{ \displaystyle \pi }を足し合わせて1であるという条件と、共分散行列{ \displaystyle \Sigma_j }が正定値であるという条件のもと、{ \displaystyle \theta }を最大にするのは困難です。つまり、この問題は解析的に解けません。

  • 隠れ変数の定義

ここで、{ \displaystyle z\in{1,...K} }のような変数{ \displaystyle z }を定義します。この変数{ \displaystyle z }を以下のように導入します。

{ \displaystyle p(x|z,\theta)=N(x|\mu_z,\Sigma_z) }・・・(1)
{ \displaystyle p(z|\theta)=\pi_z, \sum_{l=1}^K \pi_l=1 }・・・(2)

ここで、混合ガウスモデル{ \displaystyle p(x|\theta) }は以下のようになります。

{ \displaystyle p(x|\theta)=\sum_{j=1}^K p(x,z=j|\theta)\\ = \sum_{j=1}^K p(x|z=j,\theta)p(z=j|\theta)\\ = \sum_{j=1}^K \pi_jN(x|\mu_j,\Sigma_j) }

まず一行目ではxの分布がxとzの同時分布を周辺化した物で表せることを示しており、二行目では、ベイズの定理よりxの分布とzの事前分布に分けられます。そして、(1)(2)式より、zを導入した式が、混合ガウスモデルになる事が分かりました。
f:id:hiro2o2:20160212200737p:plain
上の図を見ると分かるように、隠れ変数zはどの正規分布かを表し、xとzの同時確率というのは、一つの正規分布を表します。また、それらをzについて周辺化することで混合ガウスモデルが得られるという事を表しています。

やっと本題に入ります。隠れ変数zを含めた対数尤度の式は以下のようになります。

{ \displaystyle \hat{\theta}={\rm argmax}\sum_{i=1}^I\log(\int p(x_i,z_i|\theta)dz_i)}

{ \displaystyle B[\{q_i(z_i)\},\theta] = \sum_{i=1}^I\int q_i(z_i)\log(\frac{p(x_i,z_i|\theta)}{q_i(z_i)})dz_i \le \sum_{i=1}^I\log(\int p(x_i,z_i|\theta)dz_i)}
Jensenの不等式より、最大化したい尤度よりも常に小さい尤度の下界を{ \displaystyle B[\{q_i(z_i)\},\theta]}として定義し、この下界を大きくすることで尤度の最大化を行おうというのが、EMアルゴリズムです。

{ \displaystyle B[\{q_i(z_i)\},\theta]}を最大化するために、{ \displaystyle \theta}と{ \displaystyle q_i(z_i)}を交互に求めて少しずついいものにしていきます。

・Eステップ
{ \displaystyle \theta}を固定して{ \displaystyle q_i(z_i)}を変更し、下界を最大化する

・Mステップ
{ \displaystyle q_i(z_i)}を固定して、下界を最大にする{ \displaystyle \theta}を求める

このようにEステップとMステップを繰り返すことにより、尤度を最大化し、最適なパラメータ{ \displaystyle \theta}を求めます。
f:id:hiro2o2:20160212202753p:plain
EMアルゴリズムの図的なイメージ

ただし、注意して頂きたいのが、最尤推定と同じく局所最適化などの問題を孕んでいる点など、様々な面において最尤推定の悪い部分も引き継いでいます。
しかし、実装の容易さと理解のしやすさから混合ガウスモデルのパラメータ推定によく用いられます。

混合ガウスモデルとEMアルゴリズム

機械学習

前回の記事で、単純なガウスモデルと最尤推定について紹介しました。
今回は、ガウスモデルよりも少し複雑なモデルを紹介したいと思います。

  • 混合ガウスモデル（Gaussian Mixture Model)

以下のグラフのように、ガウス分布が合わさった分布の事を混合ガウスモデルと言います。以下の例では単純に二つのガウス分布が混合した分布になります。
f:id:hiro2o2:20160211184236p:plain
上記グラフ出力の為のMatlabソースコード

clear all

%平均
mu=[4; -3];
%分散 
sigma=cat(3,4,7);
%混合比
p = ones(1,2)/2;

%1次元混合ガウスモデル
GMM = gmdistribution(mu,sigma,p);

x=-10:0.1:10;
x = transpose(x);
y = pdf(GMM,x);

plot(x,y, '-b');

上のグラフで表した1次元の混合ガウスモデルを数式で表現すると以下のようになります。
{ \displaystyle p(x|\theta)=\sum_{j=1}^K \pi_jN(x|\mu_j,\sigma_j) }
{ \displaystyle K }は混合数で今回は{ \displaystyle K=2 }，{ \displaystyle \pi }が混合比で今回は{ \displaystyle \pi_1=\pi_2=0.5 }です。また、{ \displaystyle \mu }と{ \displaystyle \sigma }はそれぞれのガウスモデルの期待値と分散になります。

混合比{ \displaystyle \pi }は
{ \displaystyle \sum_{j=1}^K \pi_j=1 } となります。
混合比{ \displaystyle \pi_1=0.2, \pi_2=0.8 }に変更した場合は以下のような混合ガウスモデルとなります。
f:id:hiro2o2:20160211195300p:plain

多変量の場合、{ \displaystyle \sigma }が分散共分散行列に置き換わり、以下の式のように表現できます。
{ \displaystyle p(x|\theta)=\sum_{j=1}^K \pi_jN(x|\mu_j,\Sigma_j) }

2次元のガウス分布を2つ用いてサンプルを生成し、EMアルゴリズムを用い、混合ガウス分布で近似した結果が以下のようになります。
f:id:hiro2o2:20160211211712p:plain

Matlabソースコードは以下の通りです。
今回のソースコードはMatlab公式のサンプルプログラムを用いています。

mu1 = [1 2];
Sigma1 = [2 0; 0 0.5];
mu2 = [-1 -2];
Sigma2 = [1 0;0 1];
rng(1); % For reproducibility
X = [mvnrnd(mu1,Sigma1,1000);mvnrnd(mu2,Sigma2,1000)];

%混合ガウス モデルを近似します。成分数を 2 に指定します。

GMModel = fitgmdist(X,2);

%近似された混合ガウス モデルの等高線上にデータをプロットします。

figure
y = [zeros(1000,1);ones(1000,1)];
h = gscatter(X(:,1),X(:,2),y);
hold on
ezcontour(@(x1,x2)pdf(GMModel,[x1 x2]),get(gca,{'XLim','YLim'}))
title('{\bf Scatter Plot and Fitted Gaussian Mixture Contours}')
legend(h,'Model 0','Model1')
hold off

混合ガウスモデルを近似するためのEMアルゴリズムの詳細については、次回の記事で紹介したいと思います。

最尤推定法について

機械学習

　前回の記事で、最尤推定法とベイズ推定の違いについて書きました。
今回は、最尤推定法に注目し、まとめていきたいと思います。

　この記事に限らず、本ブログの記事は自分も勉強しつつ書いていますので、間違いなどありましたらご指摘いただけると助かります。

　最尤推定法は、統計的機械学習で現在もよく用いられる手法の一つです。
画像から特徴量（輝度勾配など）を抽出し、得られた特徴量{ \displaystyle x }に何か確率密度関数を近似させたいとします。有限個のパラメータで記述された確率密度関数たちの事をパラメトリックモデルと言います。

　パラメトリックモデルのパラメータを{ \displaystyle θ }（いくつかのパラメータが集まったベクトル）とする時、得られた特徴量{ \displaystyle x }がうまく生起するように{ \displaystyle θ }を調節し、確率密度関数を近似することを最尤推定と言います。

　パラメータ{ \displaystyle θ }のもとで、特徴量{ \displaystyle x }が生起する確率を{ \displaystyle p(x|θ) }と表し、これを尤度と言います。最尤推定では、この尤度を最大とするパラメトリックモデルのパラメータ{ \displaystyle θ }を探すことが目的となります。

　今回、パラメトリックモデルとしてよく用いられる例としてガウスモデルを例に挙げたいと思います。
　入力{ \displaystyle x }の次元によって式は変化しますが、一般的に入力{ \displaystyle x }が{ \displaystyle n }次元の時のガウスモデルの式は以下のように表すことが出来ます。

{ \displaystyle p(x)=\frac{1}{(2\pi)^{\frac{d}{2}}|\Sigma|^\frac{1}{2}}\exp(-\frac{1}{2}(x-\mu)^t\Sigma^{-1}(x-\mu)) }

{ \displaystyle \Sigma }が分散共分散行列、{ \displaystyle \mu }が期待値を表します。簡単に言うと、{ \displaystyle \Sigma }はガウスの広がり具合を表し、{ \displaystyle \mu }はガウスの位置を表します。

matlabを使って二次元のガウス分布をプロットした例を以下に載せます。

f:id:hiro2o2:20160211125741p:plain

{ \displaystyle \mu=(0,0)}, { \displaystyle \Sigma=(4,1; 1,2)}の正規分布

f:id:hiro2o2:20160211131848p:plain

{ \displaystyle \mu=(0,0)}, { \displaystyle \Sigma=(5,1; 1,3)}の正規分布

f:id:hiro2o2:20160211131940p:plain

{ \displaystyle \mu=(3,0)}, { \displaystyle \Sigma=(4,1; 1,2)}の正規分布

 

以上の画像より、分散が大きくなると広がり、期待値が変化するとガウスが移動していることが分かると思います。

簡単のために、1次元のガウスモデルの最尤推定の例を挙げたいと思います。

最尤推定では、尤度方程式という、尤度をパラメータで偏微分したものを解くと各パラメータの最尤推定の解が得られます。

1次元のガウスモデルにおいて、尤度をパラメータで偏微分した結果は、真の期待値{ \displaystyle \mu}は標本（得られたデータ）の平均で表現でき、真の分散共分散行列は、標本の分散共分散行列で推定します。

実験で用いる真の分布は、{ \displaystyle \mu=0, \sigma=1}のガウスモデルです。
推定に用いる標本（データ）は、真の分布からランダムで生んだ標本5つを用います。

その結果、以下のような推定結果となりました。
赤線が真の分布で、青線が推定結果です。最尤推定により真の分布がある程度近似できていることが分かりました。

f:id:hiro2o2:20160211133449p:plain

標本の数を5個から100個に増やした結果が以下の通りとなります。

十分な数のデータが得られれば、真の分布が十分に近似できることが分かりました。

f:id:hiro2o2:20160211133831p:plain

今回は、シンプルなガウスモデルを用いたため、サンプル数を十分に用意すると真の分布を近似できるようになったが、もっと複雑なモデルを用いる場合（混合ガウスモデルなど）は、パラメータの初期値によっては局所的な最適解に落ち着いてしまい、真の分布が上手く近似できないという問題もあります。

ベイズ推定法と最尤推定法の違い

機械学習

ベイズ推定法と最尤推定法の違いについて
勉強した結果を簡単にまとめておきます。

ベイズってなんだっけ？って方は以下の記事を参考にして下さい。

hiro2o2.hatenablog.jp

最尤推定の枠組みではモデルのパラメータθを決定的な変数として扱います。
ベイズ推定法の枠組みでは、パラメータθを確率変数として、ベイズ推定法でパラメータθの確率密度関数を推定します。

つまり、ベイズ推定法では、たくさんのパラメータを考え、そのパラメータを事後確率{ \displaystyle P(θ|X) }で平均することで確率密度関数を近似します。

最尤推定法では、パラメトリックモデル（正規分布など）の内、尤度を最大にする確率密度関数を選びますが、真の確率密度関数と選んだパラメトリックモデルが一致していることは、現実問題ほぼないので、真の確率密度関数との間に誤差が生まれてしまう可能性があります。

一方ベイズ推定法では無数のパラメータを事後確率{ \displaystyle P(θ|X) }で平均するため、結果として最尤推定法よりも良い推定結果になる事があります。

つまり、どういうことかと言うと、ある確率密度関数を近似したい時

・最尤推定
あるパラメトリックモデルの中（二次関数など）から、尤度を最大にするパラメータ（二次関数の場合 { \displaystyle y=ax^2のa }）を選び確率密度関数を近似する

・ベイズ推定
事前分布（ここではパラメータに対する事前の情報）を用いて、尤度と事前分布を用いて事後確率（グラフの形）を求める事で近似する

 ベイズ推定を使うには事前分布（事前の情報が必要）で、事前の情報が無い場合は事前分布がどこも同じ確率になるので、最尤推定と同じ推定結果となる。
つまり、ベイズ推定は最尤推定の特殊な場合である。

 

最尤推定、MAP推定などは以下の記事が分かりやすいです。

数式なども丁寧に書かれていて分かりやすいのでぜひ参考にしてみてください。

machine-learning.hatenablog.com

 

2/11に最尤推定についての記事をUPしました。
こちらも参照してください。

http://hiro2o2.hatenablog.jp/entry/2016/02/11/134213

ベイズの定理とよく出てくる確率分布の復習

機械学習

機械学習でよく用いられるベイズの定理。 分かっているつもりでも、
あれこれはなんだったっけとなる事がしばしばあったので
今回、復習を兼ねてまとめることにします。

  • 条件付き確率

サイコロを投げて何か目が出る、コインを投げて裏か表か決まる。
こういった何か試行を行った結果を事象と言います。

事象Aが起こる確率を{ \displaystyle P(A) }、事象Bが起こる確率を{ \displaystyle P(B) }と書きます。

そして、ある事象Aが起こったという前提の元、事象Bが起こる確率を{ \displaystyle P(B|A) }
という風に書きます。これをAのもとでBが起こる条件付き確率と言います。

条件付き確率は
{ \displaystyle P(B|A)=\frac{P(A,B)}{P(A)} }

という風に表現でき、{ \displaystyle P(A,B) }をAとBの同時確率（AもBも同時に起きる確率）と言います。ベン図で書くと分かりやすいのですが、AのもとでBが起こる条件付き確率というのは、（AかつBが起きる確率）÷（Aが起きる確率）で表せる事が分かると思います。

そして、上の条件付き確率の式を{ \displaystyle P(A,B) }について解いた

{ \displaystyle P(A,B)={P(B|A)}{P(A)} }

を乗法定理と言います。

ベイズの定理は乗法定理を用いて簡単に導出できます。

{ \displaystyle P(A,B)={P(B|A)}{P(A)} }は
{ \displaystyle P(A,B)={P(A|B)}{P(B)} }とも表せます（AかつBとBかつAは同じ）
この二つの式より

{ \displaystyle {P(B|A)}{P(A)}={P(A|B)}{P(B)} }

{ \displaystyle {P(A|B)}=\frac{{P(B|A)}{P(A)}}{{P(B)}} }という風に変形でき、この式をベイズの定理と言います。

ここで、機械学習などのパターン認識でよく出てくる言葉として、事後確率、尤度、事前確率といったものがあります。ベイズの定理のAを分類したいクラス、Bをデータとすると、データが得られた元での分類したいクラスに分けられる確率なので{ \displaystyle P(A|B) }を事後確率、あるクラスにおいて、データが得られる尤もらしさなので{ \displaystyle P(B|A) }を尤度、データが得られる前の確率なので{ \displaystyle P(A) }を事前確率と言います。

 

 ある文書を特定のクラスに分類したいときなどに用いられるナイーブベイズ識別器や、事後確率が一番大きい事が一番よく起こるという考えの元用いられるMAP推定や損失を考慮したベイズ識別則などがあります。今回この記事では紹介しませんが、非常に分かりやすい解説記事がありますので、紹介しておきます。

ナイーブベイズ

aidiary.hatenablog.com

最尤推定、MAP推定

aidiary.hatenablog.com

 

  • 確率分布

この記事で紹介しようと思ったのですが、この辺で疲れてきたので今日はここまで。

畳み込みニューラルネットワークとは？

Deep Learning

今回は、Deep Learningのうち、近年画像の分野でどこの学会に行っても聞かないことはない畳み込みニューラルネットワーク（Convolutional Neural Network：CNN）について紹介したいと思います。

 

この記事は以前紹介した記事の続きとなります。

Deep Learningの基礎の基礎を知りたい方は以下のリンクから。

hiro2o2.hatenablog.jp

 

深層ニューラルネットワークでは、誤差逆伝播学習という学習手法によって、特徴量の学習が可能となりました。このような学習手法によって様々な問題への応用が可能となったが、層の数を増やすほど誤差伝播学習での学習が勾配消失問題などにより難しくなっていくという問題があります。

  •  畳み込みとは

層が多いネットワークの学習をうまく行うためのアイディアとしてあらかじめ、解きたい問題に対して結合をあらかじめ作りこむことにより学習を容易にするという手法があります。
画像にはよく畳み込みのフィルタにより特徴を計算する手法が用いられてきました。

codezine.jp

畳み込みニューラルネットワークで用いられる畳み込みも、これらの操作と同じで、画像をぼかしたり、エッジを強調したりする処理と同じです。

そして、画像を用いるネットワークの構造として、畳み込みとプーリング（解像度を粗くリサンプリングするような感じ）を繰り返す、畳み込みニューラルネットワークというネットワークが用いられるようになりました。

 

f:id:hiro2o2:20160205213405p:plain

発見と発明のデジタル博物館： 神経回路モデル「ネオコグニトロン」 (専門向け)より

 

畳み込みニューラルネットワークの元となるのは、日本の福島らが提案したネオコグニトロンというネットワークです。

このネットワークも、畳み込みとプーリングが繰り返される構造になっており、各層ごとに画像の特徴的な部分を抽出していきます。

畳み込みニューラルネットワークも、この畳込みとプーリングという特殊な操作を行う事以外、順伝播型ニューラルネットワークと同様に扱うことができます。
入力画像が与えられた時に、畳込みとプーリングにより画像の特徴を抽出し、全結合ネットワークに抽出した特徴を伝え、最終的にクラス識別を行います。

 

  • プーリングを行う利点

プーリングは、前の層の畳み込みの出力を粗くリサンプリングするようなイメージとなっており、これにより画像の多少のずれによる見え方の違いを吸収することが可能となり、少しのずれに不変な特徴量の獲得が可能となっています。

以前から画像認識で用いられてきたHOGなどの輝度勾配を用いる特徴量では画像をセルという重なりのない局所領域に分割し、それぞれの局所領域で輝度勾配のヒストグラムを計算することで画像のずれに対応していました。

 つまり、画像に特化したDeep Learningでは、畳み込みを行うフィルタの学習と画像のずれに対応するという二つを自動で行っていると言えます。

 

畳み込みニューラルネットワークは、近年、画像の分野における一般物体認識や特定物体認識において非常に良い結果を残しています。以下のスライドが非常に分かりやすいです。

www.slideshare.net

 

mnistという手書き文字認識はchainerなどのDeep Learning用のライブラリを用いて簡単に試すことが出来るので、ぜひチャレンジしてみてください。
→chainerを使って畳み込みニューラルネットワークで画像分類やってみました。
ちなみにchainerは日本のPreferredNetworksという会社で開発されたライブラリです。

chainer.org

developer.nvidia.com

 

Deep Learningを用いた歩行者画像理解（CVPR 2015論文読み）

論文紹介

CVPR2015の論文紹介です。

Deep Learningを用いた歩行者画像理解の話で、歩行者と背景の二値分類ではなく、多数のクラス（帽子をかぶっている人、カバンを持っている人、電信柱、道路、木）などへ分類するタスクに挑戦しています。

論文へのリンクは以下から

CVPR 2015 Open Access Repository

 

 

  • 近年の歩行者検出とDeep Learningの関係

これについては、以前紹介した記事で説明している通りです。

hiro2o2.hatenablog.jp

 

  • 背景

以前までのDeep Modelsは歩行者検出を2クラス分類問題として扱っていました。しかし、それでは歩行者の多様性を十分に捉えることが出来ません。

f:id:hiro2o2:20160204221108p:plain

上の画像が歩行者で、下の画像が背景です。

このように、背景とはいえ人間が見ても分類が難しいようなサンプルが現実問題ではごろごろしている状況です。

そこで、歩行者の詳細な理解が必要であると言えます。

 

  •  本論文の提案手法

f:id:hiro2o2:20160204221523p:plain

一番左が以前までの2クラス識別器です。そして、真ん中は複数の識別器（前向きの人、後ろ向きの人・・・）を用いて、識別を行う手法です。

最後に右が本論文の提案手法で、歩行者の詳細な理解と、背景の理解も行う手法です。今までと違うところは、背景も多様な状態があるので、背景も多クラスとして扱うという部分です。

また、類似した属性を有するサンプルは、高次の特徴空間においてグループ化され、分離が可能になります。

 

  • 提案手法の流れ

f:id:hiro2o2:20160204221943p:plain

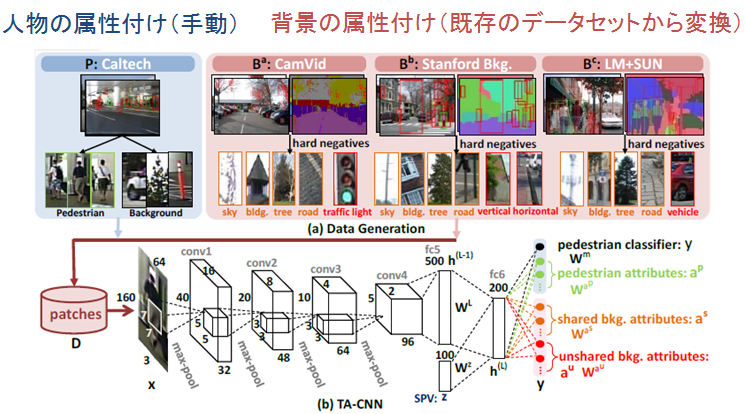
本論文では、使用するデータセットは既存のデータセットを複数組み合わせて使うことで、学習データを集める手間を減らすことが出来ています。また、それらを一緒に使う場合に競合する部分をどう扱うかも提案していました。

 

ネットワークの構造は以下のようになっています。

ネットワークはimagenetなどの一般物体認識で用いられるAlexNetを参考にし、構造を決定しています。4つの畳み込み層と4つのmax-pooling層、そして2つの全結合層があります。

また、全結合層の最後の部分には、画像の輝度勾配を特徴にするHOG特徴量を計算し、k-meansにより100次元の特徴にしたものを併用して用います。

 

f:id:hiro2o2:20160204222310p:plain

 

 

  • 感想

　今回のネットワークはAlexNetを参考にしたネットワークであまりDeepでないにも関わらず、かなりの性能を上げている。これは、データセットをうまく扱う枠組みを導入している部分と、その大量のデータセットを用いて歩行者の理解と背景の理解の2つを行っている部分で、今までの手法と比較して歩行者の検出精度が改善しているものと考えられる。